Maze sim 3d

Introduction

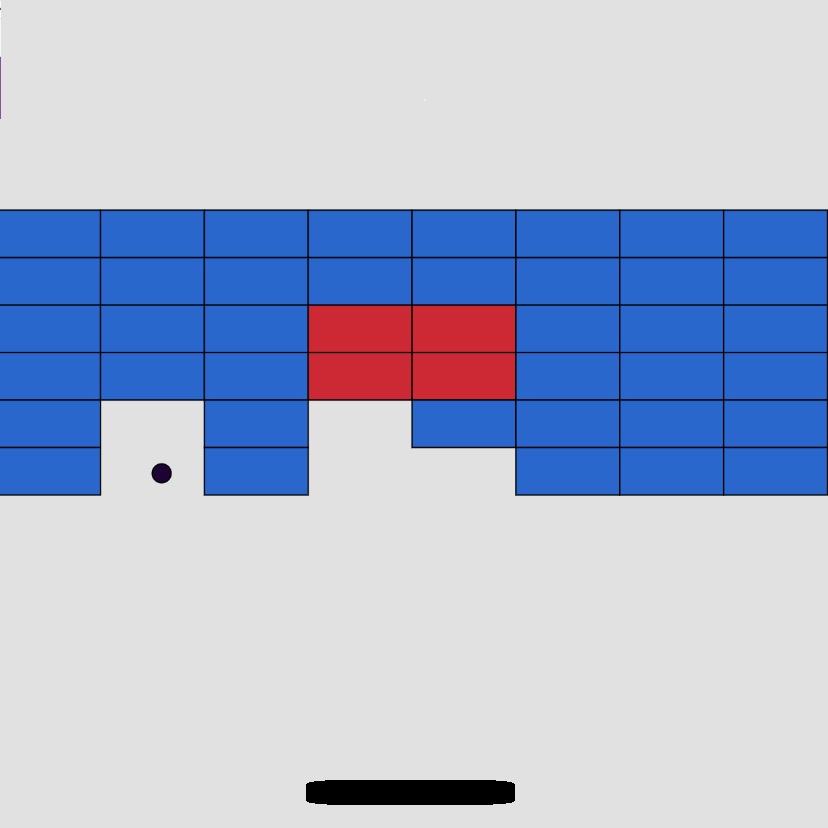
Danger! Danger! Danger!

There has been a natural disaster and people have been trapped in an urban environment with no way to get them out. Your challenge, if you choose to accept it, is to design and build a robot that can enter a dangerous collapsed building and provide aid to people in distress. Once the robot goes in there will be no means to communicate with it so it needs to be able to operate autonomously. Are you up to the challenge?

The above paragraph is a mission statement for a small challenge. The disaster scenario is represented by a maze. As a robot designer the goal is to build a robot that can navigate and complete the maze in an autonomous fashion. These rules are heavily inspired by the RoboCup Junior Rescue Maze competition.

Rules

How to solve a maze - Algorithm Style

There are many algorithms designed to complete many problems to do with maze traversal. They have their pros and their cons depending on the situation at hand. Some require prior knowledge of the maze, others only have limited memory capacity and others only focus on finding short routes from one location to another.

Left Hand Rule (Or Right Hand, if you are normal...)

The left hand rule is quite simple, always keep your left hand on the wall. If the maze is fully connected and is not disjoint as shown in the image on the right hand side the robot is guaranteed to end back at the start location having traversed the entire maze. An example of some pseudo code to accomplish something along these lines can be seen in the section below.

In the case that the walls of the maze are disjoint then the following scenario will occur. The robot will traverse the maze and return to the starting location but will not be able "to reach" the locations on the disjoint wall. This violates rule 1. In order to attempt to address this problem I came up with the Hybrid 4 algorithm.

Image showing a disjoint maze

a) Shows a maze where all walls are connected to the exterior wall. b) Shows a maze were the wall circled in red is "disjoint" from the other walls.

          
function leftHandRule(robot) {
    startPos = robot.getPos();

    while(true) {
        if(!robot.hasWallLeft()) {
            robot.turnLeft();
        } else if (!robot.hasWallFront()) {
            // do nothing
            delay(1);
        } else if (!robot.hasWallRight()) {
            robot.turnRight();
        } else if (!robot.hasWallBack()) {
            robot.turnLeft();
            robot.turnLeft();
        } else {
          // boxed in
          break;
        }

        robot.moveForward();

        if(robot.getPos() == startPos) {
            break;
        }
    }
}
          
        

Hybrid 4 Solver (1, 2 and 3???)

The Hybrid 4 maze solver is an algorithm that I developed to try and enforce full traversal of a maze. It stems from a simple wall following algorithm but with a twist. Instead of blindly following the left most wall the robot chooses to go to the left most unvisited tile. If there are no tiles to choose from check if any of the previously traversed tiles have an unvisited tile adjacent to them and go to the corresponding tile. If no tiles can be found return to the start.

There are two options that can be tweaked to produce different algorithmic behaviour: the search for a tile with unvisited neighbours, and route finding algorithm to travel between locations. Various changes to these options led to the current version of the algorithm hence the name Hybrid 4.

The current tile search method goes backwards through the list of tiles that have been traversed in visit order. This can lead to behaviours where the desired tile isn't necessarily the closest tile to the robots current position. Additionally it might be beneficial to add greater weightings to tiles that have a high number of neighbours that are also unvisited, this will lead to exploring clumps of unvisited tiles before single unvisited tiles. Again this is limited by only deciding where to explore after the robot is stuck in a location with no unvisited tiles. Planning prior to this would prevent unwanted travel.

The route finding algorithm currently doesn't use any knowledge of maze structure to find an optimal path to the goal tile. The current method is to follow the tiles backwards by visit order until the robot is at the desired tile. This can lead to the robot going around in a large spiral to return to the previous location.

Hybrid 5 Solver - A Simple Upgrade

The Hybrid 5 solver is in most ways similar to hybrid four. It has the same steps: take the left most unvisited tile until stuck, back track and go to an unvisited tile, repeat until all tiles have been visited. The main difference is that when the Hybrid 4 solver would back track to an unvisited tile it would could down through the visit order causing extremely long traversal times. The Hybrid 5 solver has a sub-optimal solution which instead goes to the lowest tile that is still higher than the desired tile location. This is not necessarily the shortest route but depending on the maze geometry can save between 10% to 20% on traversal distances. A benefit of doing traversal in this manner rather than using a shortest path finding algorithm is that it will prevent expensive search operations as it only uses data already gathered by the robot during exploration.

          
function hybrid5(robot) {
  while(!finished) {
    if(robot.checkForUnvisitedNeighbour()) {
      robot.turnToUnvisitedNeighbour();
      robot.moveForward();
      continue;
    }

    if(findTileWithUnvisitedNeighbour()) {
      robot.goToViaLowestTiles(tileWithUnvisitedNeighbour);
      continue;
    }

    robot.goTo(startPosition)
    finished = true;
  }
}