Cooper Pair Box

The Charge Qubit

In Quantum Computing a Cooper pair box is a charge qubit. This means that the amount of charge in a given location can be used to determine the state of the computer. In the case of the Cooper pair box the amount of charge that is monitored is the number of Cooper pairs.

In superconducting physics Cooper pairs, or the more formal Bardeen–Cooper–Schrieffer (BCS) pairs, are a pair of electrons that are bound together at very low temperatures. These pairs may travel together but they are not necessarily close to each other and can be hundreds of nanometres apart.

A charge qubit is generally created by forming a small island which is coupled to a reservoir of Cooper pairs through a tunnelling junction known as a Josephson Junction. The number of Cooper pairs that have tunnelled across the junction into the island gives the state of the qubit.

The Hamiltonian

The energy state of the Cooper Pair Box is described by the Hamiltonian of the system. This can be seen in Dirac (bra-ket) notation below.

$$ H = \Sigma_n (E_c(n - n_g)^2 |n \rangle \langle n| - \frac{E_J}{2} ( |n\rangle \langle n + 1 | + |n+1 \rangle \langle n|) )$$

Where \( E_C\) is the charging energy as defined by \(E_C = \frac{(2e)^2}{2(C_g + C_J)} \). \(2e\) is the charge of a Cooper pair. \(C_J\) and \(C_g\) are the Josephson junction and gate capacitance respectively.

\(n_g = \frac{C_gV_g}{2e}\) where \(V_g\) is the gate voltage of the. Finally the Josephson tunnelling energy is given by \(E_J\).

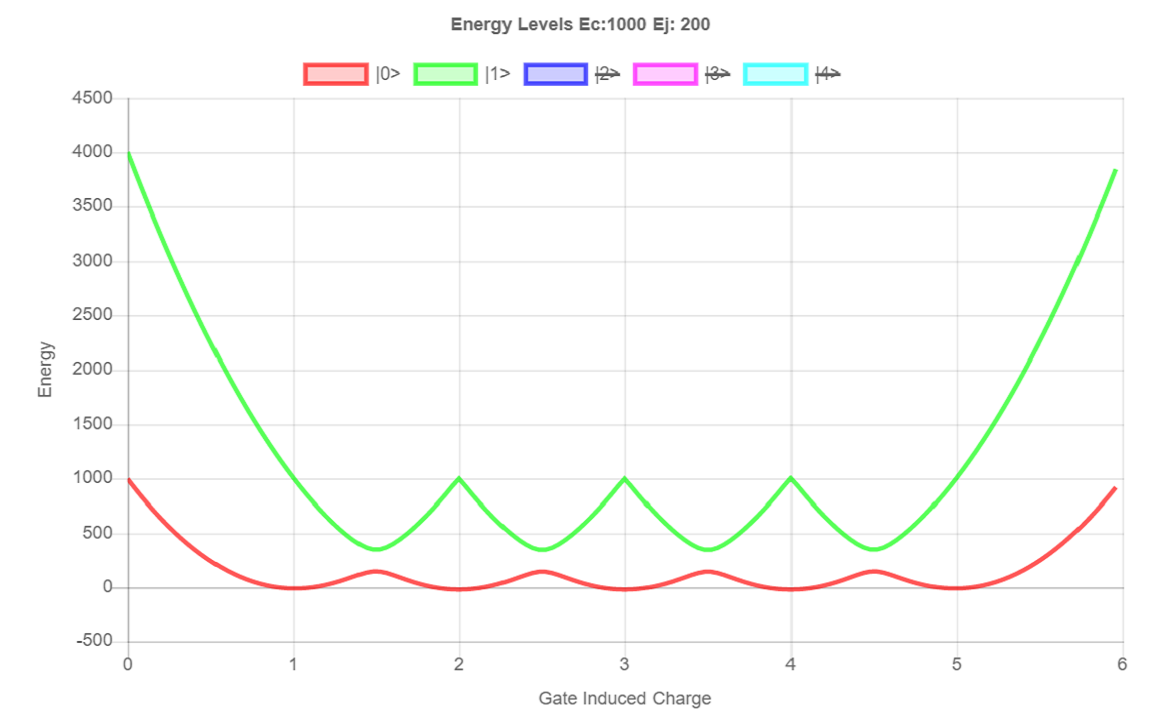
The Matrix form of the Hamiltonian can be seen below. Solving for eigen values of the Hamiltonian gives the graph plotted at the top of the page.

$$ H = \begin{pmatrix} E_c(n_0 - n_g)^2 & - \frac{E_J}{2} & 0 & 0 & ... & 0\\ - \frac{E_J}{2} & E_c(n_1 - n_g)^2 & - \frac{E_J}{2} & 0 &... & 0\\ 0 & - \frac{E_J}{2} & E_c(n_2 - n_g)^2 & - \frac{E_J}{2} & ... & 0\\ 0 & 0 & - \frac{E_J}{2} & E_c(n_3 - n_g)^2 & ... & 0\\ \vdots & \vdots & \vdots & \vdots & \ddots & ...\\ 0 & 0 & 0 & 0 & - \frac{E_J}{2} & E_c(n_n - n_g)^2\\ \end{pmatrix} $$

Special Solutions

The case where the Josephson energy \(E_J = 0\) is manifests as a series of overlapping quadratic potentials. The energy difference between one state and the next is zero. This means that Cooper pairs will travel freely between the Cooper Pair box and the reservoir. Therefore a quantum computer would not be able to do any calculations as it would effectively have no ability to remember it's previous state.

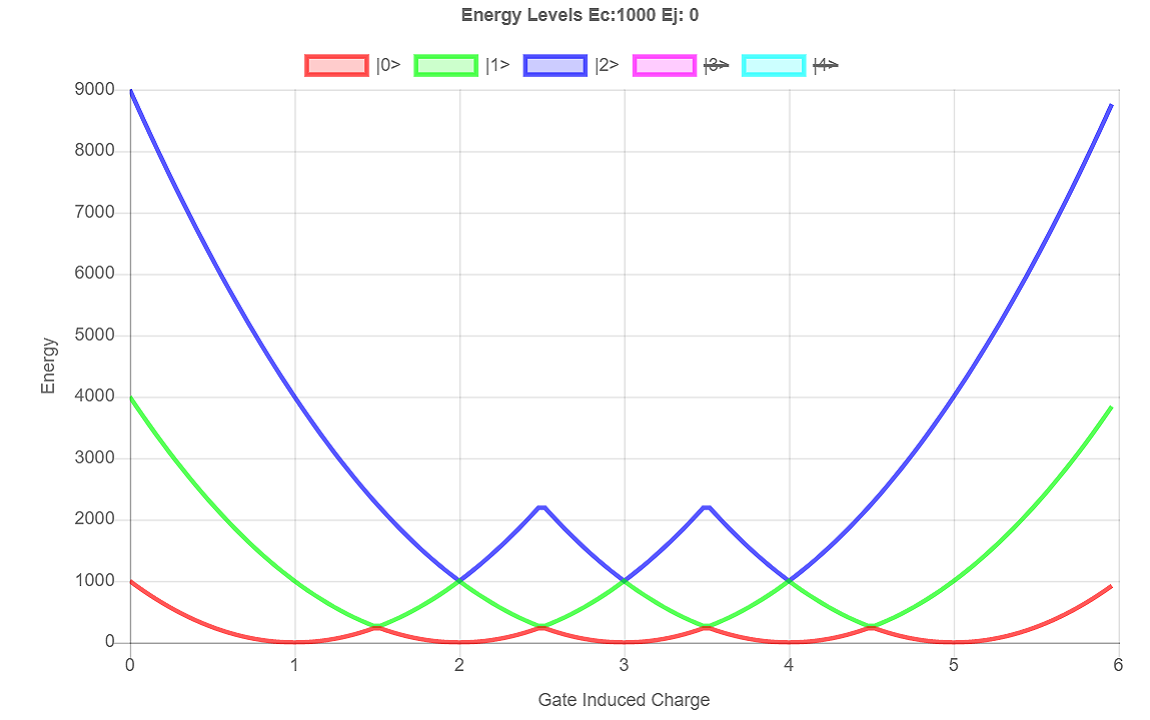
By adding a potential barrier between the reservoir and the Cooper Pair Box, in the form of a superconducting Josephson Junction, energy must be expended to change the state of the system. This can be seen on the graph as a splitting of the graph or a separation of the energy levels.

This means it now has memory. This process does not last very long and the amount of time that this is possible for is on the order of \(1-2\mu s\). This time is known as the coherence time. Understanding how to increase the coherence time is an active field of study in quantum physics.